




- Per obtenir l'adreça d'un element d'una taula, simplement s'escriu l'operador adreça `&' davant de l'element de la taula referenciat. Per exemple:
int t[10]; int *pt; pt = &t[4]; /* pt conté l'adreça de l'element t[4] */ *pt = 13; /* posem un 13 dins de t[4] , a través de pt */
- Podem fer servir els punters per recòrrer tota una taula d'elements, posicionant el punter al principi de la taula (sobre t[0]), i incrementant el contingut de la variable punter per "saltar" al següent element de la taula (els elements d'una taula s'emmagatzemen en posicions consecutives de memòria). No s'ha de tenir en compte quantes posicions de memòria ocupa cada element, ja que l'increment d'un punter s'indica amb número d'elements, i el compilador multiplica aquest número per les posicions de memòria que ocupen els elements, en funció del tipus (en el PC, un punter a int es multiplica per 2, un punter a float per 4 i un punter a char per 1).
ex 3.3: Inicialitzar tots els elements d'un vector de 10 elements a través d'un punter (del mateix tipus que els elements de la taula):
#include <stdio.h>
void main(void)
{
int t[10];
int *pt, i;
pt = &t[0]; /* posicionar pt sobre el primer element del vector */
for (i=0; i<10; i++) /* repetir 10 vegades ... */
{
*pt = 13; /* col.loca un 13 sobre l'element que està apuntant */
pt++; /* pt apuntarà al següent enter (sumar 2 a pt) */
}
for(i=0; i<10; i++) printf("%d\n",t[i]); /* escriu el vector */
}
- Una altra forma d'accedir a una taula a través de punters és fer servir el punter com a base i indicar un desplaçament fins a l'element que es vol referenciar. Una altra vegada el desplaçament s'expressarà en número d'elements, i el compilador s'encarrega de convertir-lo a desplaçament en posicions de memòria (en funció del tipus dels elements i del Hardware que es fa servir). Per expressar l'adreça base d'una taula podem fer-ho donant l'adreça del seu primer element o, simplement, amb el nom de la taula sense cap índex.
ex 3.4: Aquest és el mateix algorisme que l'exemple anterior, però fent servir el mode d'accés base més desplaçament (mode d'adreçament):
#include <stdio.h>
void main(void)
{
int t[10];
int *pt, i;
pt = t; /* pt pren per valor l'adreça base del vector */
for(i=0; i<10; i++)
/* accés punter base més desplaçament */
*(pt + i) = 13; /* (cal posar el punter i el desplaçament entre
parèntesi, abans de posar l'asterisc) */
for(i=0; i<10; i++) printf("%d\n",t[i]);
}
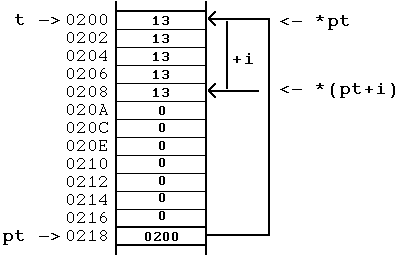
- Un aspecte curiós del llenguatge C és que permet intercanviar els mètodes de referència d'elements dels punters i de les taules. És a dir, podem posar el desplaçament respecte a un punter entre claudàtors, i podem posar l'índex d'un vector sumat a l'adreça del vector i tot junt precedit d' un asterisc. Cal tenir present, però, que el punter és variable (pt++; està permés) i el nom de la taula no (t++ no està permés). Exemples:
pt[i] = 13; <=> *(pt + i) = 13
printf("%d\n", *(t + i)); <=> printf("%d\n", t[i]);
- Editeu el fitxer EXERCI_2.C i substituïu els interrogants per les instruccions que implementin el que es demana en els comentaris adjunts. El resultat ha de ser:
ts = "Es kui no m'e$coltes mai!"
- La utilització de punters com a base de matrius segueix el mateix principi que sobre vectors, però cal tenir en compte que el desplaçament de l'índex de files ha d'anar multiplicat pel número d'elements que hi ha a cada columna (no obstant això, ara tampoc cal multiplicar el desplaçament total per la mida dels elements).
- Implementarem, per exemple, l'algorisme que posa a zero tots els elements d'una matriu de 9 x 6 enters llargs (4 bytes per element):
#define N_Fil 9
#define N_Col 6
long ml[N_Fil][N_Col];
int i,j;
for(i=0; i<N_Fil; i++)
for(j=0; j<N_Col; j++)
ml[i][j] = 0;
- Podem substituir l'accés als elements ml[i][j] mitjançant l'ús del punter pl, i el càlcul corresponent al desplaçament de l'element en funció dels índexos:
ex 3.5: Accés a matrius mitjançant punters i desplaçaments:
#define N_Fil 9
#define N_Col 6
void main(void)
{
long ml[N_Fil][N_Col];
int i,j;
long *pl = ml;
for(i=0; i<N_Fil; i++)
for(j=0; j<N_Col; j++)
*(pl+ i*N_Col+ j) = 0;
}
També es pot escollir una representació de tipus matriu per als punters, és a dir:
*(pl+ i*N_Col+ j) = 0; <=> pl[i][j] = 0;
- La pregunta que es planteja és per què fer servir punters si obtenim el mateix resultat que amb les taules. La resposta és que es permet un mecanisme molt lligat a les possibilitats dels Llenguatges Màquina. És a dir, els accesos amb punters corresponen als modes d'adreçament, i per tant, es pot fer una programació més òptima si es pensa en aquests termes. Per exemple, per inicialitzar una matriu tota a zeros, els elements de la qual sabem que estan emmagatzemats consecutivament, podriem implementar la inicialització com un sol bucle, de la següent forma:
for(i=0; i < N_Fil*N_Col; i++) *(pl + i) = 0;
Anant una mica més enllà, podem implementar l'accés amb mode d'adreçament registre indirecte autoincrementat, en comptes de registre base més desplaçament:
for(i=0; i < N_Fil*N_Col; i++, pl++) *pl = 0;
- Pel cas de matrius de 3 o més dimensions es pot aplicar el mateix principi, tenint en compte que els índexos es multiplicaran pel rang de l'índex immediatament inferior. Exemple:
*( p3D + ((i * N_J) + j) * N_K + k)




